LeetCode日常-简单-面试题57 - II. 和为s的连续正数序列

本文最后更新于：2020年9月27日 晚上

题目

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。
序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。
示例 1：
  输入：target = 9
  输出：[[2,3,4],[4,5]]
示例 2：
  输入：target = 15
  输出：[[1,2,3,4,5],[4,5,6],[7,8]]
限制：
1 <= target <= 10^5

自解

1
2
3
4
5
6
7
8
9
10
11
def findContinuousSequence(self, target: int) -> List[List[int]]:
    resoult = list()
    for left in range(1, target):
        right = left
        sum_ = 0
        while sum_ < target:
            right = right+1
            sum_ = sum(range(left, right))
            if sum_ == target:
                resoult.append(list(range(left,right)))
    return resoult

思路

逐个数字遍历，窗口逐个变大。找到相等记录。

大佬解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def findContinuousSequence(self, target: int) -> List[List[int]]:
    i = 1 # 滑动窗口的左边界
    j = 1 # 滑动窗口的右边界
    sum = 0 # 滑动窗口中数字的和
    res = []

    while i <= target // 2:
        if sum < target:
            # 右边界向右移动
            sum += j
            j += 1
        elif sum > target:
            # 左边界向右移动
            sum -= i
            i += 1
        else:
            # 记录结果
            arr = list(range(i, j))
            res.append(arr)
            # 左边界向右移动
            sum -= i
            i += 1

    return res

思路

什么是滑动窗口

滑动窗口可以看成数组中框起来的一个部分。在一些数组类题目中，我们可以用滑动窗口来观察可能的候选结果。当滑动窗口从数组的左边滑到了右边，我们就可以从所有的候选结果中找到最优的结果。
对于这道题来说，数组就是正整数序列 [1,2,3,…,n]。我们设滑动窗口的左边界为 i，右边界为 j，则滑动窗口框起来的是一个左闭右开区间 [i,j)[i, j)[i,j)。注意，为了编程的方便，滑动窗口一般表示成一个左闭右开区间。在一开始，i=1, j=1 ,滑动窗口位于序列的最左侧，窗口大小为零。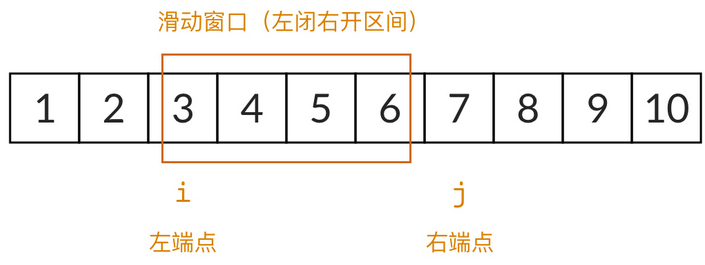

滑动窗口的重要性质是：窗口的左边界和右边界永远只能向右移动，而不能向左移动。这是为了保证滑动窗口的时间复杂度是 O(n)。如果左右边界向左移动的话，这叫做“回溯”，算法的时间复杂度就可能不止 O(n)。

在这道题中，我们关注的是滑动窗口中所有数的和。
当滑动窗口的右边界向右移动时，也就是 j = j + 1，窗口中多了一个数字 j，窗口的和也就要加上 j。
当滑动窗口的左边界向右移动时，也就是 i = i + 1，窗口中少了一个数字 i，窗口的和也就要减去 i。
滑动窗口只有 右边界向右移动（扩大窗口） 和 左边界向右移动（缩小窗口） 两个操作，所以实际上非常简单。

如何用滑动窗口解这道题

要用滑动窗口解这道题，我们要回答两个问题：
  第一个问题，窗口何时扩大，何时缩小？
  第二个问题，滑动窗口能找到全部的解吗？

第一个问题，窗口何时扩大，何时缩小？

  当窗口的和小于 target 的时候，窗口的和需要增加，所以要扩大窗口，窗口的右边界向右移动
  当窗口的和大于 target 的时候，窗口的和需要减少，所以要缩小窗口，窗口的左边界向右移动
  当窗口的和恰好等于 target 的时候，我们需要记录此时的结果。设此时的窗口为 [i,j)，那么我们已经找到了一个 i 开头的序列，也是唯一一个 i 开头的序列，接下来需要找 i+1 开头的序列，所以窗口的左边界要向右移动

第二个问题，滑动窗口能找到全部的解吗？


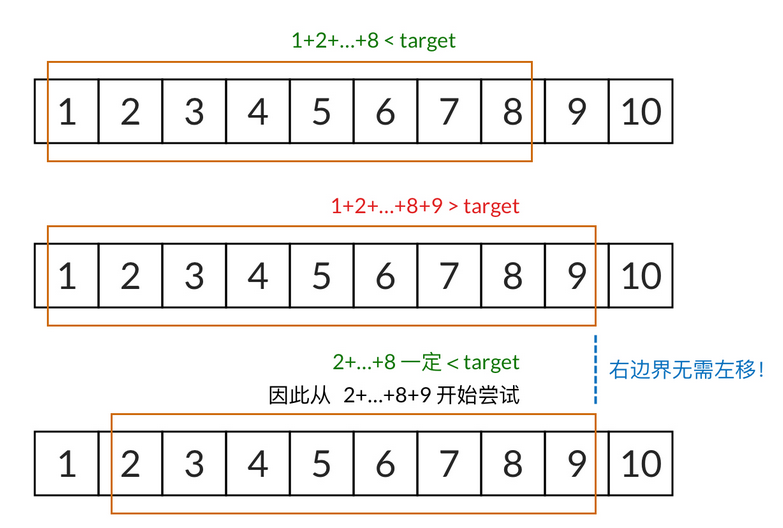
  我们一开始要找的是 1 开头的序列，只要窗口的和小于 target，窗口的右边界会一直向右移动。
  假设 1+2+⋯+8 小于 target，再加上一个 9 之后， 发现 1+2+⋯+8+9 又大于 target 了。这说明 1 开头的序列找不到解。此时滑动窗口的最右元素是 9。

接下来，我们需要找 2 开头的序列，我们发现，2+⋯+8<1+2+⋯+8<target。这说明 2 开头的序列至少要加到 9。那么，我们只需要把原先 19 的滑动窗口的左边界向右移动，变成 29 的滑动窗口，然后继续寻找。而右边界完全不需要向左移动。

以此类推，滑动窗口的左右边界都不需要向左移动，所以这道题用滑动窗口一定可以得到所有的解。时间复杂度是 O(n)O(n)O(n)。

注：这道题当前可以用等差数列的求和公式来计算滑动窗口的和。不过我这里没有使用求和公式，是为了展示更通用的解题思路。实际上，把题目中的正整数序列换成任意的递增整数序列，这个方法都可以解。

真·大佬解法

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        res = []
        for n in range(2, target+1):
            temp = target - n*(n-1)//2
            if temp <= 0:
                break
            if not temp % n:
                a_1 = temp // n
                res.append([a_1 + i for i in range(n)])
        return res[::-1]

O(√target)

解题思路
一个以 a1 为首项，以 1 为公差，以 n 为项数的等差数列的和为 target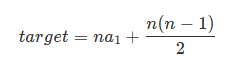

转化为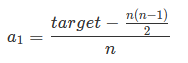

目标是找出所有满足条件的 n、a1 对，
思路是对 n 从 2 开始遍历（题目要求最少是 222 个数），验证 a1 是否为正整数。
有一个问题是 n 遍历到多少呢？
其实不需要特地去算 n 的上限，随着 n 的递增，a1 递减，当 a1<=0 时跳出循环即可。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof
作者：nettee
链接：https://leetcode-cn.com/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/solution/shi-yao-shi-hua-dong-chuang-kou-yi-ji-ru-he-yong-h/
作者：erik_chen
链接：https://leetcode-cn.com/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/solution/shu-xue-wen-ti-shu-xue-jie-jue-by-erik_chen/